In a previous post, I looked at whether the GC Dice Rollers produce truly random results. In this one, I ask: What is the likely distribution of dice rolls in a round of APBA Golf?
Will the dice rolls be fairly evenly distributed or will certain numbers appear quite a lot more or less than the others? I used the GC’s Dice Roller for these analyses. Here is the frequency of each of 500 APBA dice rolls:
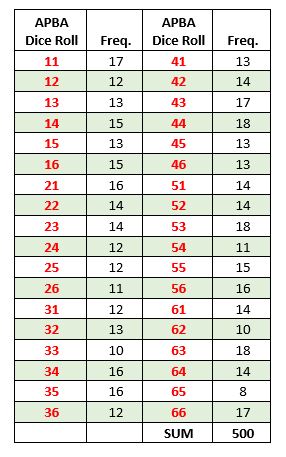
You can see that in this trial, the most frequent rolls were 44, 53, and 63 (18 each). The least frequent roll was 65 (8 times). The expected frequency for each dice roll number is 13.9 (500/36).
In a typical round for two players, there might be on the order of 400 to 500 dice rolls, including those for shots, lies, and wind. Therefore, don’t be surprised if you get more than an average number of rolls for the same number. It may be a “good” number or a “bad” number, or it may happen with more than one number. In fact, it would be unusual if some number DIDN’T appear significantly more often than the others. The same is true for some number(s) appearing significantly less often than average.
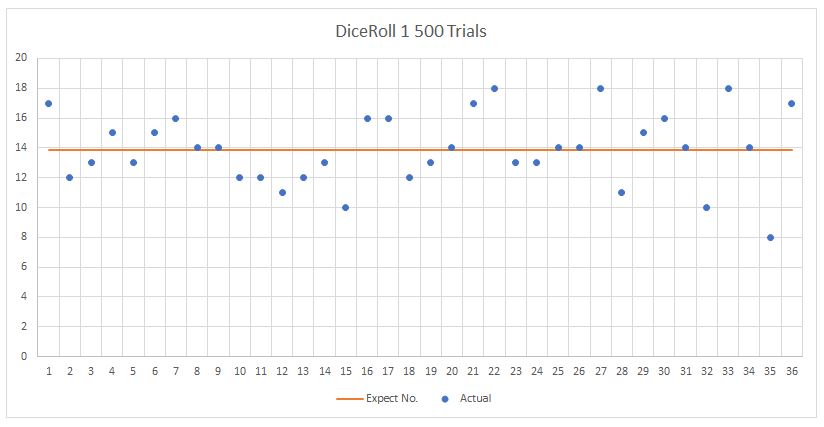
Here’s a scatterplot of those 500 dice rolls, showing the frequency by which they occurred. The numbers 1 – 36 represent the 36 possible roll results with 1 = 11, 2 = 12, etc. The straight line is the expected frequency of each dice roll. As you can see, there is quite a lot of variability due to a relatively small sample size (500).
What happens if we greatly increase the number of dice rolls? By 100,000 rolls, we have a much more stable result. On average, the actual frequencies are much closer to the expected frequency, as the image below shows.
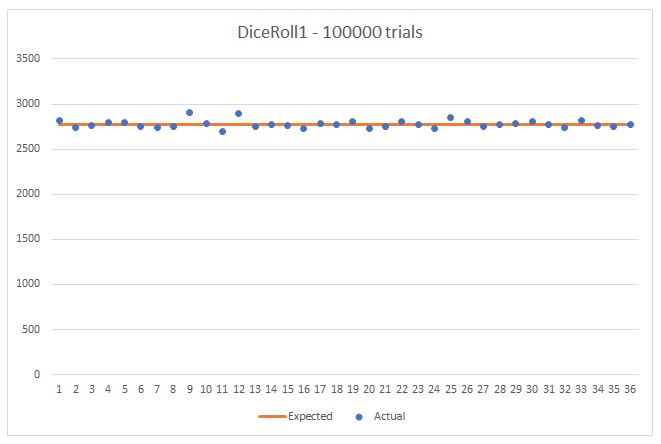
Note that some roll results still appear more than average and some less, but the amount of variability is far smaller. In this data set, the mean Standard Deviation (SD/Mean), expressed as a percent, is 1.6%. By contrast, the 500-roll trial mean Standard Deviation is 17%. More trials, less sample error, no surprise.
What does all this tell us? In any given round, a player may get more than a few repeat numbers. Over the long run, the Game Caddie, using Excel’s random number generator, does produce predictable, stable results for dice rolls. Given how much one plays, the long run might be defined in terms of a player’s lifetime, however.
This article and test is impressive Scott.
Maybe it will influence me for the futur ?